On November 10, László Babai, the George and Elizabeth Yovovich Professor in the Departments of Mathematics and Computer Science, presented the first of three seminars outlining a new algorithm. If confirmed, the algorithm will solve the Graph Isomorphism (GI) problem, one of the most prominent open problems in theoretical computer science, in quasi-polynomial time.

Scott Aaronson, associate professor of computer science at MIT, described Babai’s finding on his blog as “what might be the theoretical computer science result of the decade.”

The GI problem is as follows: Given two finite graphs (sets of points connected with lines), does an isomorphism exist between the graphs?

To understand isomorphism between two graphs, consider the analogy of a social network within a dormitory. If we assume that each student occupies a single room in a dorm, then his or her room can be considered a vertex in a graph. Then imagine each relationship as being represented by a line connecting the room of the two students involved. This representation forms a graph. Now imagine that all of the students moved into a different dorm. If all of the relationships are retained, then the graph of the new dorm is considered isomorphic to the original dorm’s graph, even though the positional arrangement of the students may have changed.

According to this analogy, the graph isomorphism problem can then be restated as follows: Prove or disprove that the original dorm described and another dorm are isomorphic and, therefore, represent the same social network. That is, the vertexes, or students, are connected by relationships in the same way.

Consider the lines in Figure A.

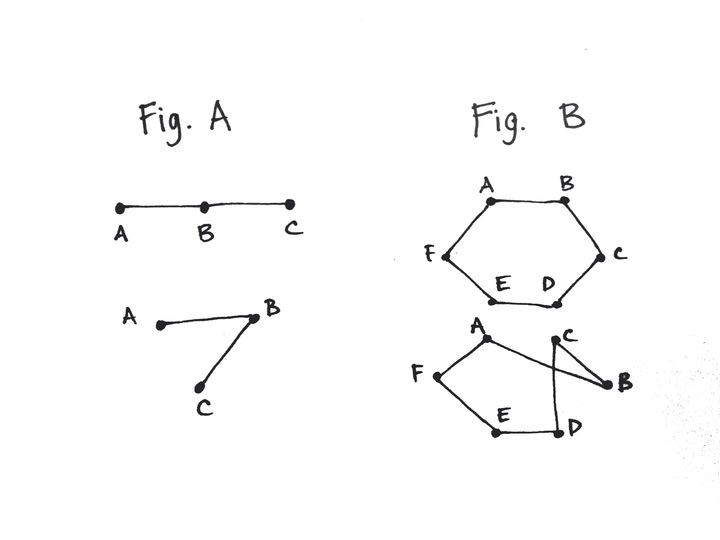
These lines are different in shape, but they represent the same relationship between the points; the same connections between points exist in both graphs, so this simple graph is isomorphic.

Let’s consider a more complicated graph. (Figure B)

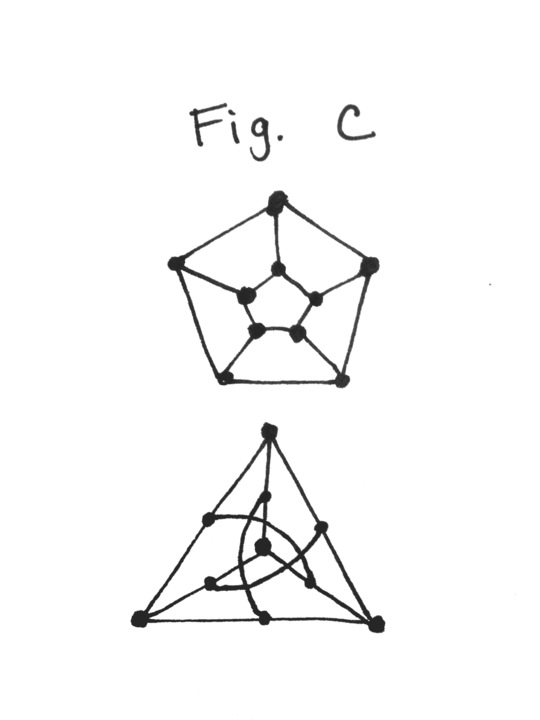
The graph in Figure C is also isomorphic, though less obviously so.

Although the peer review process is just beginning, the algorithm, if confirmed, constitutes a major breakthrough in the fields of theoretical computer science and combinatorics.

Previously, the most efficient algorithm, also formulated by Babai in 1983, solved the GI problem in exponential time. Calculating the solution requires more time and resources to solve as the problem grows in complexity. Computations in exponential time quickly become infeasible and can require years of computational time with today’s hardware.

For any two graphs, Babai’s new algorithm claims to compute the solution in quasi-polynomial time, which is much faster than exponential time. This is particularly exciting in the world of theoretical computer science because there has been no progress in determining the difficulty of the GI problem for more than 30 years.

In the course of the next few months, Babai’s paper will be extensively reviewed by fellow experts in the field in hopes of confirming or refuting his finding.