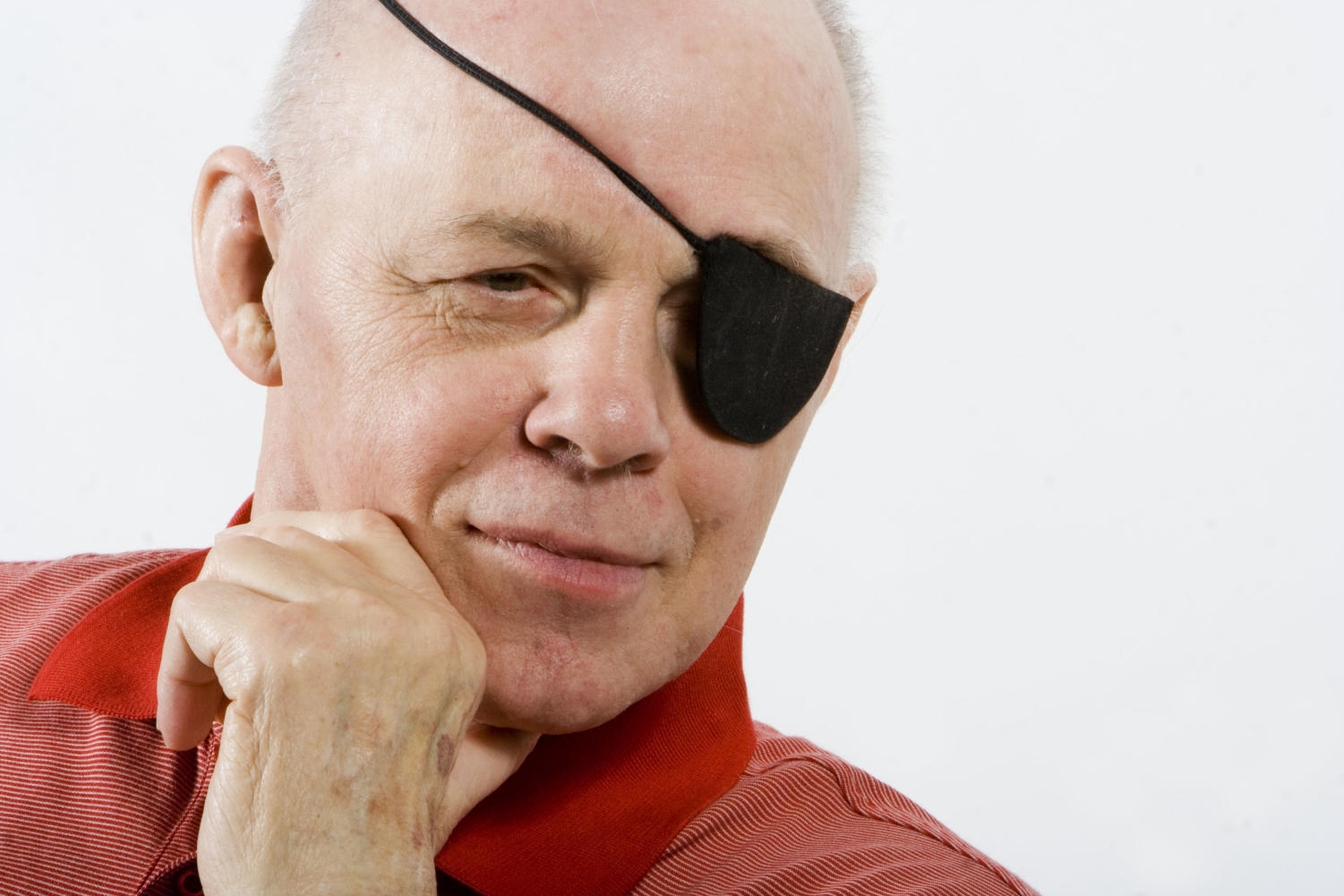
P aul Sally, Jr., is a powerful man. At 76 years of age, the professor and director of undergraduate studies in mathematics says he works out daily and can bench press 150 pounds. He keeps 30-pound dumbbells under the desk in his Ryerson office; broach the subject of strength training for too long, and he’ll challenge you to do curl-ups with them. Yet these are just the physical manifestations of Sally’s far greater internal might. He’s tough enough, for example, to joke about his marshmallow Peep alter-ego the same way he laughs off the disease that took away his legs and most of his eyesight. Maybe it helps Sally to know that he’s had the last laugh. He ambles about his classrooms on two titanium prosthetics and barks commands and encouragement at students, making it clear that nothing can dent his more than 50-year commitment to mathematics education. Where life sought to cut him down to size, Sally came back with a larger-than-life “math pirate” persona. His track record has earned him armfuls of teaching awards, as well as a place among legends at the University of Chicago.
Supriya Sinhababu: Back in April, the alumni magazine held a contest asking alumni to make dioramas, using marshmallow Peeps, that expressed school spirit in some way. And one of the submissions was a diorama of your classroom. You were represented as a marshmallow Peep bunny with an eye patch, and one of your legs was a Tootsie Roll. How do you feel about being immortalized as a Peep?
Paul Sally: Oh, I think it’s marvelous. I think the way I would be immortalized is through satire, there is no question about that…
SS: You’ve said that people view it as a “badge of honor” to not be good at math.
PS: Yeah, well. Ignorance is bliss.
SS: You’ve also said that they’d never say the same thing about not knowing how to read. I was wondering why you think it’s become socially acceptable to not be good at math, and what can be done about it?
PS: …First of all, to actually be good at math you have to practice, you have to take it seriously, and you have to be willing to spend time working at it. And all of these are very difficult for students and for humans in general. And they don’t understand that you should never confuse activity with achievement. Many people spend a lot of time early in their math careers, early in their math days, in the classroom, working at it extensively, saying, “I worked three hours on math last night.” Well, if they didn’t achieve anything, that’s activity, that’s not achievement…. And if you don’t get it right, you have failed.
…If you’re working on a certain project in a lab, and you set up the protocol correctly, then whatever the results, you can publish them. “I did this in the lab, and this is what happened.” But see, in mathematics you can’t do that. You have to set out to solve a problem or prove a theorem, and by the time you get through, if you don’t have a proof, you cannot actually publish your results, making apologies for your inability to prove the theorem. You simply have to confess that you couldn’t do it….
SS: What do you think can be done to give people a greater appreciation of math?
PS: Well, at an early stage—and we work intensively on this project—you can give teachers of mathematics in the elementary grades, and even high school, a firmer appreciation of mathematics…. The University just opened a new UTEP program that works with elementary school teachers who are going—it actually works with our own undergraduates who are going to become teachers in the Chicago Public Schools. And there’s a firm appreciation of what mathematics means in that program…. To teach real mathematics, you have to know some. And the other thing is, you should approach it with several strategies in mind as kids come up with questions in the classroom. And you can only do this through extensive content knowledge.
SS: Given that I’m not a math-y person, and I might not understand it at a very high level, I was wondering if you could explain what the biggest intellectual challenge facing the field of mathematics is right now?
PS: …That’s hard to say. At the upper level of mathematics, there are a number of very difficult problems in various areas of mathematics—harmonic analysis, differential equations, things like that, number theory. And these are extremely challenging problems. One of the things about mathematics, of course, is that you cannot discuss your current research in mathematics in the New York Times Sunday Magazine…. True detailed discussion of the mathematics itself would not sell a lot of copy…. But I would say that the richness of the field of mathematics continually grows. There are problems that are unsolved and need to be solved in order for the field to progress…
SS: You served as the academic consultant for the film Proof when that was being filmed here. I was wondering what that means?
PS: It doesn’t mean anything…. John Madden, who was the director…sat on my couch and said, “My! This is a copious couch.” Then we went on to discuss the nature of the film. I had already seen it in the theater [as a play], so I already knew what it was all about. We discussed the mathematical background, and the fact that when it was first written, there was this big unsolved problem which was obviously called Fermat’s Theorem. And Fermat’s Theorem had since been solved, so we had to find a new emphasis for the unsolved problem. And that led to some very interesting discussions. I also met Gwynie [Gwynyth Paltrow].
SS: Oh yeah?
PS: Oh yeah! A lovely young lady. I told her she was the second best-looking graduate school student in mathematics since I had been here. The best one was my wife, by far. I made sure she understood that. I met Tony, Hopkins, Anthony Hopkins. He’s just what you’d expect, sort of a rough guy. And they did a lot of filming. It was sort of a big to-do and all that, and when they finally made the film, virtually none of it appeared.
SS: Oh really?
PS: Yeah. There was a collage of teaching and scenes from the University of Chicago, and then right out here, as a matter of fact, the stairs here, right down the hall, Jake Gyllenhaal came running down from the third floor—this was after they discovered the manuscript—and this was all filmed out here, but it never appeared in the film. But Jake is a good guy…. Seemed to have a good head on his shoulders…
SS: To the extent that a Hollywood film can, did you feel like Proof ended up having any kind of real mathematical backbone?
PS: No, it’s pretty funny—look, the film was not about mathematics. The play was a much more realistic approach to the problem. But there were some strange parts to it that didn’t ring true. But it’s okay. Who knows about mathematicians and who cares about mathematicians anyway? We’re regarded as a pretty bizarre type of human being who lives somewhat outside the ordinary pale of human existence.
SS: Do you agree with that characterization?
PS: Of course not! That’s a lot of crap.
SS: So, are there any good math movies? Or math novels, or math poetry, or anything like that?
PS: …I mean, cryptography, Alan Turing and World War II—there’ve been some interesting movies about that sort of thing. But to my knowledge, no specific movie about mathematics has any significance whatsoever—as far as mathematics goes. I mean if you want to watch Anthony Hopkins and Gwynie Paltrow and people like that, that’s great. But you can go to any movie and watch them.
SS: I know that cell phones that go off in your class tend to be confiscated, stomped on, and/or thrown out the window.
PS: Could I also be quoted? They also piss me off.
SS: Noted. Now, as obnoxious as they are, what makes you hate them so much that you’d actually destroy them?
PS: They are an interference to human existence. It will be only a matter of time before kids are born with cell phones sewn to their ear. Maybe, actually growing from their ear.
SS: So you don’t own a cell phone?
PS: I do not. Nor will I ever own a cell phone. There is no reason why I should be accessible to the entire human race 24 hours a day, seven days a week…. Except there is one tale I’ve told, the story about the kid who thought he was going to miss my final—
SS: Yeah, and you rebooked his flight.
PS: Yeah. I changed his airline reservation.
SS: So that’s actually true?
PS: Yeah! He claims not to remember it, but I happen to have confronted him with this. It’s actually true. Southwest Airlines. Called it right from the classroom. Changed the reservation. So that was one good use of cell phones.
SS: “Yo, Sally!” seems to be your address of choice, to the point that you’ve promised not to hang up on a student if they call at midnight with a math question and they preface that question with “Yo, Sally.” Is there any special meaning to this?
PS: It’s a special form of address. I don’t like someone calling me at midnight saying, “Well, Professor Sally, this is Alex Jojo.” But if you call me and you say “Yo, Sally,” it means you’re part of the club. There’s something called Sally’s Gang. Once you get into it you can never leave. And, that means you can call me, any time day or night, anywhere you are in the world or anywhere I am in the world and say “Yo, Sally,” and you’re in business. I also use it in class because I can’t see the class. If someone raises their hand, they might as well be waving at the moon. But if they say “Yo, Sally,” I know they have a question. I’d rather that than “Hey, you” or “I have a question.” “Yo, Sally.” Bingo.
SS: You’ve worked with a pretty remarkable age range of students for a tenured professor. You’ve worked with kids from middle school to adult teachers. Are the challenges and rewards of teaching have some basic similarities across age ranges?
PS: Absolutely. At every level, it’s the same thing: Enlighten people about mathematics. No question. Now, there’s the alphabet, right? Goes from A to Z. Some people you enlighten in D-E-F. Other people you enlighten at L-M-N. Then the students in MATH 207-8-9 you enlighten at the X-Y-Z level, along with the graduate students. In other words, the idea about teaching is to learn how to teach any audience at any level, what will enhance their knowledge of mathematics and take them to the next level. So the reason for teaching, that I’ve loved teaching, everyone from seven-year-olds to adults to everything in between, is that you learn so much about people and how they understand mathematics. If you teach one audience all the time, you never get that perspective.
SS: Do you mind if I ask you a question about your legs?
PS: My legs? Ooh, you like them?
SS: Yeah, I do.
PS: Robo-legs, they call them, baby, woohoo! Yeah, go ahead, what about them?
SS: Well I imagine you could just become taller, sort of on a whim.
PS: I could be seven feet.
SS: Okay! Well have you ever wanted to come into class one day suddenly like a foot taller than the day before?
PS: Six-three, 200, is the best you could be, let me tell you. Well I can’t say that—when I was a senior in college, I was about six-three, 185, and since then I’ve sort of put it on. A lot of it’s muscle. No, I don’t want to be anything but six-three. Now the other side of that is, I don’t want to be five-eight. This really angers five-eight people when I say that, but I don’t want to be five-eight! I’ve been six-three my whole life. As a matter of fact, when I had my second leg cut off, my surgeon and prosthetist got together and said, “Look, Paul, if we lower your center of gravity, you’ll have much more balance.” I said, “Are you kidding me?” They really thought they were going to shorten my height by about five or six inches. When you learn to exist and address the world at a certain height—and six-three is a very nice height to address the world from—you want to stay there.
About an hour after our conversation, I went back to Paul Sally’s office to ask him a final question.
SS: You told me that you’re 95-percent blind. I imagine this requires you to do an enormous amount of math in your head.
PS: I do.
SS: How do you do that?
PS: I’m one powerful son of a bitch.
SS: You must be!
PS: I’ve always had a strong memorization capacity—you have to to be a mathematician. There’s no question, you have to remember millions of things. Ever since I lost the sight in my left eye, oh, 35 years ago, in 1975. And then my right eye has been pretty good. It’s all from diabetes, of course. It’s one of life’s joys. Then I had a bad cataract in the early part of this decade, and that really obscured my vision. But I’ve had to memorize huge things when I write books. And my memory has expanded. My mind is like…it’s like a steel trap, okay? And that’s exactly the way I feel. I can remember enormous amounts of material, and then forget it immediately until I sort of need that recollection power again. So it’s an interesting observation, that that’s something I’ve had to acquire. And I get around fine. I get around without a cane here, and in my apartment…
SS: So would you say you have a photographic memory, then?
PS: I think photographic memory means you see something once, and you remember it.
SS: That’s true, that’s true.
PS: It’s not the same thing as having a voluminous memory, where you can remember and recall facts about a large amount of material right on the spot.
SS: So if someone’s describing a problem to you, do you write it on some kind of internal chalkboard?
PS: Well look, there’s two parts to it, Supriya. One is, if the problem is related to something I already know, then I click in and make connections automatically. If it’s a brand new topic, I need to go over it two or three different times until there’s something embedded in my mind that allows me to make connections to it. It’s a very interesting process to relate to, because I’ve been writing books a mile a minute…. And I remember a large part of the material that’s in these books.